1943. Мосты

Дан неориентированный граф. Найдите все мосты в нем.

Вход. Первая строка содержит два натуральных числа n и m – количество вершин и ребер графа соответственно (n ≤ 2 * 10⁴, m ≤ 2 * 10⁵). Следующие m строк содержат описание ребер по одному на строке. Ребро номер i задается двумя натуральными числами b_i, e_i (1 ≤ b_i, e_i ≤ n) – номерами вершин, которые оно соединяет.

Выход. Первая строка должна содержать количество мостов b в заданном графе. На следующей строке через пробел выведите b целых чисел – номера ребер, которые являются мостами, в возрастающем порядке. Ребра нумеруются с единицы в том порядке, в котором они поступают на вход.

Пример входа	Пример выхода
6 7 1 2 2 3 3 4 1 3 4 5 4 6 5 6	1 3

РЕШЕНИЕ

графы – мосты

Анализ алгоритма

Запустим поиск в глубину с расстановкой меток d[v] и up[v]. Из вершины v или её потомка есть обратное ребро в её предка тогда и только тогда, когда найдётся такой сын to, что up[to] < d[v]. Если для некоторого ребра дерева (v, to) выполняется равенство up[to] = d[v], то в поддереве поиска с вершиной v найдется обратное ребро, приходящее точно в v. Если же up[to] > d[v], то ребро (v, to) является мостом. Никакое обратное ребро мостом быть не может.

Пример

Граф, приведенный в примере, имеет следующий вид:

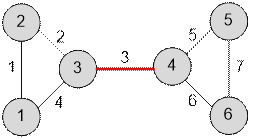
Реализация алгоритма

Поскольку количество вершин в графе велико, будем хранить граф в виде списка смежности graph. Массив used используется для отмечания уже пройденных вершин. Для решения задачи будем также использовать два дополнительных массива d и up. Во множестве Bridges будем собирать номера ребер, являющихся мостами. Для каждого входного ребра (a, b) будем запоминать его номер в отображении mp.

vector<vector<int> > graph;

vector<int> used, d, up;

set<int> Bridges;

map<pair<int,int>, int> mp;

Функция Edge возвращает ребро – пару вершин (a, b), где a < b.

pair<int,int> Edge(int a, int b)

{

if (a > b) swap(a,b);

return make_pair(a,b);

}

Функция dfs реализует поиск в глубину. Расставляем метки d[v] и up[v]. Вершина p является предком v в дереве поиска.

void dfs (int v, int p = -1)

{

used[v] = 1;

d[v] = up[v] = time++;

for (int i = 0; i < graph[v].size(); i++)

{

int to = graph[v][i];

if (to == p) continue;

if (used[to])

up[v] = min (up[v], d[to]);

else

{

dfs (to, v);

up[v] = min (up[v], up[to]);

if (up[to] > d[v]) Bridges.insert(mp[Edge(v,to)]);

}

}

}

Поиск мостов совершаем вызовом функции FindBridges.

void FindBridges(void)

{

time = 1;

for(int i = 1; i <= n; i++)

if (!used[i]) dfs(i);

}

Основная часть программы. Читаем входной граф. Для каждого ребра (a, b) запоминаем его номер в отображении mp. Это нам нужно чтобы потом выводить мосты не как пары вершин, которые они соединяют, а как номера входных ребер.

scanf("%d %d",&n,&m);

graph.resize(n+1); used.resize(n+1);

d.resize(n+1); up.resize(n+1);

for(i = 1; i <= m; i++)

{

scanf("%d %d",&a,&b);

graph[a].push_back(b); graph[b].push_back(a);

mp[Edge(a,b)] = i;

}

Запускаем поиск мостов. Номера ребер – мостов заносим во множество Bridges.

FindBridges();

Выводим количество мостов. В следующей строке выводим номера ребер – мостов в возрастающем порядке.

printf("%d\n",Bridges.size());

for(iter = Bridges.begin(); iter != Bridges.end(); iter++)

printf("%d ",*iter);

printf("\n");